2019. 4. 7. 22:41ㆍ알고리즘
이진탐색트리란 이진탐색(binary search)과 연결리스트(linked list)를 결합한 자료구조의 일종입니다. 이진탐색의 효율적인 탐색 능력을 유지하면서도, 빈번한 자료 입력과 삭제를 가능하게끔 고안됐습니다.
예컨대 이진탐색의 경우 탐색에 소요되는 계산복잡성은 O(logn)으로 빠르지만 자료 입력, 삭제가 불가능합니다. 연결리스트의 경우 자료 입력, 삭제에 필요한 계산복잡성은 O(1)로 효율적이지만 탐색하는 데에는 O(n)의 계산복잡성이 발생합니다. 두 마리 토끼를 잡아보자는 것이 이진탐색트리의 목적입니다.
이진탐색트리는 다음과 같은 속성을 지니며 아래 그림과 같습니다.
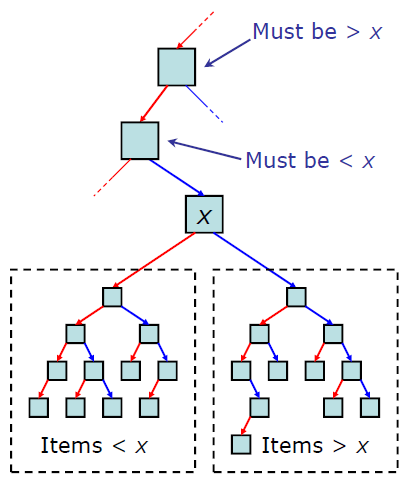
- 완전이진트리이다.
- 각 노드의 왼쪽 서브트리에는 해당 노드의 값보다 작은 값을 지닌 노드들로 이루어져 있다.
- 각 노드의 오른쪽 서브트리에는 해당 노드의 값보다 큰 값을 지닌 노드들로 이루어져 있다.
- 중복된 노드가 없어야 한다.
- 왼쪽 서브트리, 오른쪽 서브트리 또한 이진탐색트리이다.
이진탐색트리를 순회할 때는 중위순회(inorder) 방식을 씁니다. (왼쪽 서브트리-노드-오른쪽 서브트리 순으로 순회) 이렇게 하면 이진탐색트리 내에 있는 모든 값들을 정렬된 순서대로 읽을 수 있습니다. 다음 예시와 같습니다.
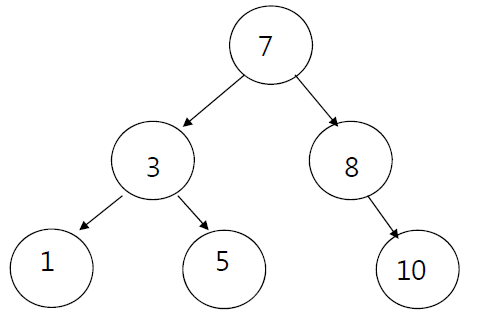
중위순회 : 1, 3, 5, 7, 8, 10
한편 트리 순회와 관련 자세한 내용은 이곳을 참고하시면 좋을 것 같습니다.
이진탐색트리의 핵심 연산은 검색(retreive), 삽입(insert), 삭제(delete) 세 가지입니다.
탐색
아래 이진탐색트리에서 10을 탐색(retreive, search)한다고 가정해 봅시다. 이진탐색트리는 부모노드가 왼쪽 자식노드보다 크거나 같고, 오른쪽 자식노드보다 작거나 같다는 점에 착안하면 효율적인 탐색이 가능합니다.

우선 루트노드(7)와 10을 비교합니다. 10은 7보다 큽니다. 따라서 왼쪽 서브트리(1, 3, 5)는 고려할 필요가 없습니다. 탐색공간이 대폭 줄어든다는 얘기입니다. 이번엔 오른쪽 서브트리의 루트노드(8)과 10을 비교합니다. 10은 8보다 큽니다. 따라서 오른쪽 서브트리의 루트노드(10)과 10을 비교합니다. 원하는 값을 찾았습니다.
삽입
이번엔 삽입 연산을 살펴 보겠습니다. 새로운 데이터는 트리의 잎새노드에 붙입니다. 예컨대 탐색 예시에서 제시한 트리에 4를 추가한다고 가정해 봅시다. 아래와 같습니다.

그런데 위 트리에서 7과 3사이에 4를 추가해도 이진탐색트리의 속성이 깨지지 않음을 확인할 수 있습니다. 하지만 이진탐색트리가 커질 경우 이렇게 트리의 중간에 새 데이터를 삽입하게 되면 서브트리의 속성이 깨질 수 있기 때문에 삽입 연산은 반드시 잎새노드에서 이뤄지게 됩니다
삭제
이진 탐색 트리 관련 알고리즘 중 가장 복잡합니다. 삭제도 먼저 삽입과 마찬가지로 탐색을 먼저 해야합니다.. 삭제하길 원하는 키 값이 트리 안의 어디에 위치하는지를 알아야 삭제할 수 있기 때문입니다. 노드를 탐색했다면, 아래의 3가지 경우를 고려해야 한다. 삭제시 발생할 수 있는 상황 3가지입니다..
- 삭제하려는 노드가 단말노드일 경우 (자식 노드가 없을 경우)
- 삭제하려는 노드가 하나의 서브트리만 가지는 경우 (왼쪽 혹은 오른쪽 둘 중 하나만)
- 삭제하려는 노드가 두 개의 서브트리를 모두 가지고 있는 경우
먼저 첫 번째 경우에 대해 생각해봅시다. <삭제하려는 노드가 단말노드일 경우>

단말 노드를 삭제하는 행위는 매우 간단합니다. 부모 노드를 찾아서 부모 노드 안의 해당 링크(그림의 경우 오른쪽 링크) 필드를 NULL로 만들어서 연결을 끊어주면 됩니다. 동적으로 할당된 노드였을 경우, 메모리 반납을 하고 링크필드를 NULL로 만들어주면 됩니다.
이번엔 두 번째 경우를 살펴봅시다. <삭제하려는 노드가 하나의 서브트리만 가지는 경우>
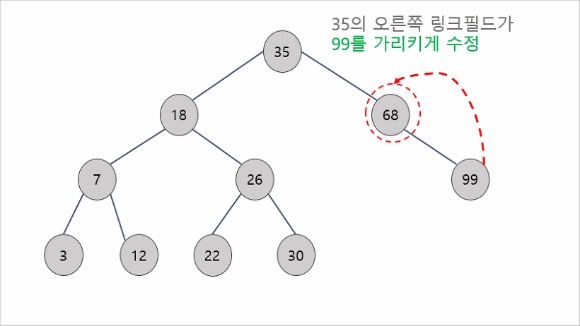
68을 가지고 있는 노드를 삭제하고자 합시다. 이것 또한 간단한데, 35를 가지고 있는 부모 노드의 오른쪽 링크 필드가 99를 가리키게 수정하면 됩니다. 동적할당된 노드였다면, 68을 먼저 반납해주고 부모의 오른쪽 링크에 99를 붙여주면 됩니다..
이제 가장 복잡한 세 번째 경우를 살펴봅시다. <삭제하려는 노드가 두 개의 서브트리를 모두 가지고 있는 경우>

18을 삭제하려 합니다. 삭제한 이후에 35를 가지고 있는 부모 노드의 왼쪽 링크필드를 어떤 노드에 연결시켜야 할까요? 결론부터 말하면 왼쪽 서브트리에 있는 값 중 가장 큰 값, 혹은 오른쪽 서브트리에 있는 값 중 가장 작은 값을 가지고 있는 노드를 연결시켜주면 됩니다.
이러한 판단의 근거는 트리의 변동성을 최소화하기 위함에 있습니다. 18이 있는 상태에서 중위 순회를 한다고 가정해봅시다. 중위 순회의 순서는 우리가 알다시피 L V R입니다. 순회를 하던 도중 12까지 이르렀다고 가정합니다. 12 다음에는 어딜 방문할까요? 그렇습니다. 18을 방문합니다. 18다음에는 22를 방문합니다. 즉, 12 - 18 - 22 순서로 방문하게 됩니다. 12와 22는 각각 삭제할 노드의 중위 선행자 후속자에 속합니다. 이들을 선택해서 18자리를 대체하면 트리의 변동성을 최소로 할 수 있습니다. 딱 하나만 바꾸면 트리가 정상적으로 작동합니다.
22를 선택했다고 가정해봅시다. 그러면 우리가 할 일은 삭제되는 노드의 오른쪽 서브 트리에서 왼쪽 자식 링크를 타고 NULL이 나올 때까지 게속 진행하면 됩니다. 그렇게 찾아낸 값을 35의 왼쪽 링크 필드에 이어주고 22의 왼쪽 링크필드를 7에, 오른쪽 링크필드를 26에 연결해주면 됩니다.
코드해석
(Chiken class)
package treeproject;
public class Chiken {
int price;
String name;
int id;
public Chiken(int id, String name, int price){
this.id = id;
this.name = name;
this.price = price;
}
public void fry() {
System.out.println(name+"("+id+")"+"을 배달한다");
}
public void delivery() {
System.out.printf("%s(%d) 배달을 간다", this.name, this.id);
}
}
일단 치킨이라는 클래스를 만들었다. 치킨 클래스에서 치킨은 int 값으로 가격과 id를 받고있으며 string으로 name을 받고있다. 생성자를 id값과 name price값을 this로 만들어줬다.
(Node Class)
package treeproject;
public class Node {
public Node left;
public Node right;
public Chiken chiken;
public Node(Chiken chiken) {
this.chiken = chiken;
}
이진탐색 트리를 만들기 위해서 노드를 만들었다. 이진탐색트리의 노드는 위에서도 설명했지만 숫자가 루트보다 작으면 왼쪽 크면 오른쪽이라는 체계를 가진다 그러므로 노드안에 Left와 Right를 넣고 노드 안에 넣을 데이터 값으로 위에 클래스로 만든 Chiken을 받도록 만들었다. 마찬가지로 Node에대한 생성자도 만들었다.
(add Fn)
public void add(Chiken chiken) {
if(this.chiken.id > chiken.id) {
if(this.left == null)this.left = new Node(chiken);
else this.left.add(chiken);
}
else {
if(this.right == null)this.right = new Node(chiken);
else this.right.add(chiken);
}
}
삽입 함수를 만든것이다 데이터값으로 클래스로 만들었던 치킨을 받아서 추가한다. 예를들어 id값이 6인 치킨과 id값이 8인 치킨있다면 처음 root는 Node root = new Node(new Chiken(8, "스노윙치킨", 18000)); 이런식으로 넣기때문에 따로 만들지 않는다. this.chiken.id값은 root의 치킨 id값인 8을 의미하며 chiken.id 는 add로 받는 id값을 말하는 거기때문에 들어오는 치킨 id를 의미한다. id값이 6이라면 root의 id값보다 작기때문에 this.left == null 이라는것은 root의왼쪽 노드값이 존재하지 않는다면 지금 왼쪽에 id가 6인 치킨값으로 생성하라는 소리이며 아닐경우 그 왼쪽값에서 다시 add함수로 들어가서 확인하라는 재귀적이게 짠 함수이다.
(search Fn)
public Node search(int id) {
if(this.chiken == null) {
return null;
}
if(this.chiken.id == id) {return this;}
if(this.chiken.id > id) {
return this.left.search(id);
} else{
return this.right.search(id);
}
}탐색 함수에 대해서 보자 만약 id값으로 root는 8에 6 5 13 24가 add되었다고 생각해보자 여기서 add함수로 만들어지는 모습은

이런식으로 만들어진다 root 8의 left에 6이 6의 left에 5가 8의 right에 13이 13의 right에 24가 연결되었다
만약 여기서 6을 찾는다고 한다면 위 탐색 함수에서 this.chiken.id는 처음 root의 id이므로 8이다 8>6이므로 왼쪽으로 넘어가고 this.left로 search함수에 들어가게된다. 무슨소리냐면 위에 그림에보이는 6이 this가 되서 다시 search함수가 시작된다고 생각하면된다. 그리고 this.chiken.id == id 로 들어가면 return this로 현재 노드를 내보내고 재귀함수는 종료된다.
(del Fn)
public void del(Node parent, int id) {
if(this.chiken.id == id) {
//자식 노드가 없을때
if(this.left == null && this.right == null) {
if(parent == null) {
this.chiken = null;
}
if(parent != null) {
if(this.chiken.id > parent.chiken.id) {
parent.right = null;
} else {
parent.left = null;
}
}
}
//왼쪽 자식노드가 없을때 오른쪽만 있을떼
else if(this.left == null && this.right != null) {
if(this.chiken.id > parent.chiken.id) {
parent.right = this.right;
} else {
parent.left = this.left;
}
return;
//오른쪽 자식노드가 없을때 왼쪽만 있을때
}else if(this.right == null && this.left != null){
if(this.chiken.id > parent.chiken.id) {
parent.right = this.left;
} else {
parent.left = this.left;
}
return;
}
//자식노드 둘다 있을때
else if(this.right != null && this.right != null) {
if(parent == null)
{
Node rightSubTree = this.right;
Node leftSubTree = this.left;
Node current = this;
current = getSuccessor(this);
current.right = rightSubTree;
if (current == rightSubTree) // 지우려는 노드의 오른쪽 sub tree 에 노드가 하나밖에 없는 경우
current.right = null;
current.left = leftSubTree;
return;
}
if(parent != null) {
if(this.chiken.id > parent.chiken.id) {
parent.right = this.left;
} else {
parent.left = this.left;
}
}
}
this.left = this.right;
}
else if(this.chiken.id > id ) {
this.left.del(this,id);
}
else if(this.chiken.id < id ){
this.right.del(this,id);
}
}parent는 부모노드로 처음에 null값으로 들어간다. 예를들어 아까 사진을 가져와보자

이런식으로 이진트리가 들어가있다고 쳤을때 5를 지우려고 해보자 그럼 root.del(null, 5); 이런식으로 메인함수에서 실행할것이다. root는 8이다 if(this.chiken.id == id) 에 포함되지않는다 8>5이다 그러므로 밑으로 내려가서 else (this.chiken.id> id)로 들어가 다시 this.left.del(this. id); 를 실행시킨다 여기서 this 는 root로 이게 parent로 들어가는것이고 id는 똑같은 5가 들어가고 this.left인 6에서 다시 del 함수가 실행된다. 그럼 이제 다시 del 함수로 들어가게 된다면 parent는 8 this는 6이되고 id는 똑같이 5이다 그럼 6>5 이기때문에 다시 this.left.del(this, id)가 실행되고 다시 parent 는 6 this 는 5 id도 5 가된다. 그러므로 if (this.chiken.id==id)를 성립하므로 안으로 들어가 여기서 자식노드는 없으므로 if(this.left == null && this.right == null)로 들어가서 parent = 6 this = 5 이므로 5>6 이다 그러니 parent 노드의 왼쪽을 null값으로 만들면 간단하게 왼쪽 단일노드함수인 5는 삭제되는것이다.
대강 이런식으로 함수가 이루어진다. 자식이 하나인경우 중간에 13을 지우는 경우는 parent의 right 에 this의 right를 붙여서 자기자신 없애고 8과 24가 연결되게 만든다.
자식이 두개인경우는
public Node getSuccessor(Node deleteNode){
Node successor = null;
Node successorParent = null;
Node current = deleteNode.right;
while(current != null){
successorParent = successor;
successor = current;
current = current.left;
}
if(successor != deleteNode.right){
successorParent.left = successor.right;
successor.right = deleteNode.right;
}
System.out.println(successor);
return successor;
}자식이 두개있는 노드에 자신의 오른쪽에서 가장 작은값을 구하는 함수이다. 이 함수로 값을 구한뒤 자기 자신의 왼쪽과 오른쪽을 미리 지정해둔뒤 자신에 이 함수로 구한 값을 복사해서 넣고 저장해둔 왼쪽 오른쪽 값을 다시 이어붙여주면된다.
메인함수 코드
package treeproject;
public class tree {
public static void main(String[] args) {
//add함수
Node root = new Node(new Chiken(8, "스노윙치킨", 18000));
root.add(new Chiken(6, "몰라치킨", 2000000));
root.add(new Chiken(5, "빠리치킨", 19000));
root.add(new Chiken(13, "맛초킹", 17000));
root.add(new Chiken(24, "레드윙", 19000));
//search 함수
Node search = root.search(8);
System.out.println(search);
search = root.search(24);
System.out.println(search);
search = root.search(5);
System.out.println(search);
search = root.search(6);
System.out.println(search);
search = root.search(13);
System.out.println(search);
//del 함수
root.inOrderTraverse(root);
System.out.print("\n");
root.del(null,6);
root.inOrderTraverse(root);
System.out.print("\n");
root.del(null,5);
root.inOrderTraverse(root);
System.out.print("\n");
root.del(null,13);
root.inOrderTraverse(root);
System.out.print("\n");
root.del(null,24);
root.inOrderTraverse(root);
System.out.print("\n");
root.del(null,8);
root.inOrderTraverse(root);
}
}
처음 root함수는 add함수로 넣은게아니라 직접 값을 넣어주었고 나머지는 add로 추가해주었다.
search함수는 5개를 다 출력해보기위해서 다 쓰게되었다.
del 함수는 가장 왼쪽먼저 출력되는 중위순회를 사용하여 제대로 지워지는지 확인하기위해서 넣게되었다.
중위순회 코드
public void inOrderTraverse(Node focusNode) {
if (focusNode != null) {
if(focusNode.chiken == null) {
System.out.print(" ");
return;
}
inOrderTraverse(focusNode.left);
System.out.print(focusNode.chiken.id + " ");
inOrderTraverse(focusNode.right);
}
}
출력값

출력값이다 하나씩 지워지는것을 볼수있으며 마지막 8이 지워지고 null값이되어 공백만 출력된것도 볼 수 있다.
'알고리즘' 카테고리의 다른 글
| 해시 (체이닝, 개방주소) (0) | 2019.04.29 |
|---|---|
| kd-트리 (0) | 2019.04.29 |
| B트리 (0) | 2019.04.29 |
| 레드블랙트리 (자가균형 이진탐색트리) (0) | 2019.04.15 |