2019. 4. 29. 18:21ㆍ알고리즘
개요
º Balanced Tree란?
- 이진 검색 트리의 문제점은 좌우 균형이 맞지 않으면 비효율적. 트리의 성능은 곧 트리의 depth인데, 좌 또는 우로 치우친 경우 O(logN) → O(n^2)까지 성능이 느려질 수 있다.
- Balanced Tree는 삽입, 삭제 시 필요하면 스스로 균형을 유지한다.
- ex) AVL Tree, 2-3(-4) Tree, Red-Black Tree, B-Tree 등
- 항상 (최악의 경우에도) O(logN) 성능을 보장
º B-Tree란?
- 하나의 노드에 여러 자료가 배치되는 트리 구조
- 한 노드에 최대 m개의 자료가 배치되면 → 'M차 B-Tree'
(단, 모든 노드에 항상 m개의 자료가 배치되어야 하는 것은 아님)
- m이 짝수냐 홀수냐에 따라 알고리즘이 다르다.
- 2-3 Tree는 2차 B-Tree와 같고, 2-3-4 Tree는 3차 B-Tree와 같다.
#2. 규칙
1. 어떤 노드의 자료 수가 N개라면, 그 노드의 자식의 수는 N+1이어야 한다.
2. 각 노드의 자료는 정렬된 상태여야 한다.
3. 노드의 자료 Dk의 왼쪽 서브트리는 Dk보다 작은 값들이고, Dk의 오른쪽 서브트리는 Dk보다 큰 값들이어야 한다.
(설명)

- A B 노드는 C보다 작은 값이다.
- D E 노드는 C보다 크고 F보다 작은 값이다.
- G H 노드는 F보다 큰 값이다.
4. Root 노드는 자식이 있다면, 적어도 2개 이상의 자식을 가져야 한다.
5. Root 노드를 제외한 모든 노드는 적어도 m/2개의 자료를 가져야 한다.
(5차 B-Tree라면 적어도 2개 이상)
6. 외부 노드(leaf)로 가는 경로의 길이는 모두 같다.
(= 외부 노드는 모두 같은 레벨에 있다.
7. 자료는 중복될 수 없다.
#3. B-Tree 삽입 알고리즘
- 자료는 항상 Leaf 노드에 추가된다.
- Leaf 노드 선택은 삽입될 키의 하향 탐색에 의하여 결정된다.
- 추가될 Leaf 노드에 여유가 있다면, 그냥 삽입
- 여유가 없다면 노드를 분할한다.
- 분할을 위해서는 키 하나를 부모로 올려야 한다.
- 부모에 여유가 없다면? : 삽입을 위한 하향 탐색을 하면서 꽉 찬 노드는 미리미리 분할을 해줘야 한다.
BTree_Insert(value) {
while (currentNode is not leaf) {
if (currentNode is full) split(currentNode);
currentNode = proceedToChildNode;
}
if (currentNode is full) split(currentNode);
currentNode -> addNodeValue(value);
}
1) Root 노드의 분할

2) 일반 노드의 분할
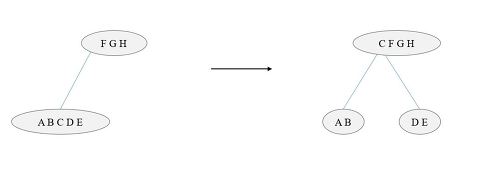
#4. B-Tree 삭제 알고리즘
- 삭제하려는 자료가 있는 노드는 삭제 후에도 m/2 이상의 자료수를 유지해야 한다.
Case #1. 외부 노드 삭제
1) 빌리기 : 형제가 m/2보다 많은 자료를 가지고 있는 경우

2) 결합하기 : 형제에서 빌릴 수 없는 경우
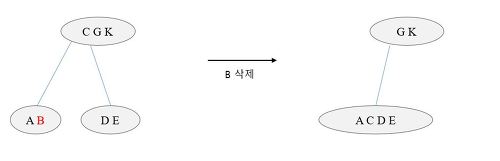
Case #2. 내부 노드 삭제
- 삭제하려는 자료가 존재하는 노드가 내부 노드인 경우, 대체키를 찾아 대체해야 한다. (왼쪽 서브트리의 가장 큰 값 or 오른쪽 서브트리의 가장 작은 값)
- 삭제를 위한 하향 탐색을 하면서 자료수가 m/2 이하인 노드는 빌리기/결합하기
#5. B-Tree 성능
- M차 B-Tree의 높이는 log_m/2 N 이하이다.
- 검색 시 각 노드당 최대 M번의 순차 검색
- 삽입 / 삭제 / 검색 성능 : O(logN)
º B-Tree는 외부 검색에 적합함
- 하나의 노드 크기를 Disk I/O 단위의 크기로
- 순차 검색과 트리 검색의 이점을 취함
코드
/*
프로그램 설명 : C++로 구현한 B-Tree입니다.
*/
#include <iostream>
#define M 5
using namespace std;
// BTree의 노드 구조체를 선언합니다.
struct BTreeNode // Public과 동일한 구조체 선언입니다.
{
int *data; // 노드에 들어갈 자료의 배열입니다.
BTreeNode **childPtr; // 노드 포인트의 배열입니다.
bool leaf; // 리프 노드인지 확인합니다.
int n; // 자료의 개수를 의미합니다.
}*root = NULL, *np = NULL, *x = NULL;
// 노드를 초기화하는 함수입니다.
BTreeNode * init()
{
int i;
np = new BTreeNode; // 객체를 할당합니다.
np->data = new int[M]; // M개까지의 데이터를 가질 수 있습니다.
np->childPtr = new BTreeNode *[6]; // M + 1개의 자식 노드입니다.
np->leaf = true; // 기본적으로 리프 노드입니다.
np->n = 0; // 자료의 개수는 0개입니다.
for(i = 0; i < 6; i++)
{
np->childPtr[i] = NULL; // 각각의 자식 노드를 초기화해줍니다.
}
return np;
}
// 현재 트리를 보여주는 순회 함수입니다.
void traverse(BTreeNode * p)
{
cout << endl;
int i;
// 즉, 첫번째 자식 노드부터 가장 마지막 자식 노드까지 전부 밑으로 내려가는 것입니다.
for(i = 0; i < p->n; i++)
{
// 리프 노드가 아니라면 더 밑으로 내려갑니다.
if(p->leaf == false)
{
traverse(p->childPtr[i]);
}
// 데이터를 출력합니다.
cout << " " << p->data[i];
}
// 리프 노드가 아니라면 더 밑으로 내려갑니다.
if(p->leaf == false)
{
traverse(p->childPtr[i]);
}
cout << endl;
}
// n개 존재하는 데이터 배열 데이터를 정렬하는 함수입니다.
void sort(int *p, int n)
{
int i, j, temp;
for(i = 0; i < n; i++)
{
for(j = i; j <= n; j++)
{
if(p[i] > p[j])
{
temp = p[i];
p[i] = p[j];
p[j] = temp;
}
}
}
}
// 자식을 분할하는 함수입니다.
int splitChild(BTreeNode *x, int i)
{
// x노드를 분할하여 np1과 np3을 할당합니다.
int j, mid;
BTreeNode *np1, *np3, *y;
/*
분할된 형태는 다음과 같습니다.
x -> 왼쪽으로 가고
np3 -> 그 오른쪽으로 가고
np1 -> x와 np3의 부모 노드가 됩니다.
*/
np3 = init();
np3->leaf = true;
// x의 부모 노드가 없어 새롭게 부모 노드를 만들어주는 경우입니다.
if(i == -1)
{
// M의 중간값을 기준으로 분할합니다.
mid = x->data[M / 2];
x->data[M / 2] = 0;
x->n--;
np1 = init();
// np1는 부모노드이므로 리프 노드가 아닙니다.
np1->leaf = false;
x->leaf = true;
for(j = M / 2 + 1; j < M; j++)
{
// np3는 x의 오른쪽 부분 노드를 가져갑니다.
np3->data[j - (M / 2 + 1)] = x->data[j];
np3->childPtr[j - (M / 2 + 1)] = x->childPtr[j];
np3->n++;
// x는 반 쪼개서 왼쪽 부분 노드만 가지고 갑니다.
x->data[j] = 0;
x->n--;
}
// x의 모든 자식 노드를 NULL로 만듭니다.
for(j = 0; j < M + 1; j++)
{
x->childPtr[j] = NULL;
}
np1->data[0] = mid;
np1->childPtr[np1->n] = x;
np1->childPtr[np1->n + 1] = np3;
np1->n++;
// 루트 노드로 설정해줍니다.
root = np1;
}
// 이미 부모 노드가 있는 경우입니다.
else
{
y = x->childPtr[i];
mid = y->data[M / 2];
y->data[M / 2] = 0;
y->n--;
for(j = M / 2 + 1; j < M; j++)
{
// np3은 x의 오른쪽 자식 부분만 가져갑니다.
np3->data[j - (M / 2 + 1)] = y->data[j];
np3->n++;
y->data[j] = 0;
y->n--;
}
x->childPtr[i + 1] = y;
x->childPtr[i + 1] = np3;
}
return mid;
}
// a라는 원소를 삽입하는 함수입니다.
void insert(int a)
{
int i, temp;
x = root;
// 만약에 루트 노드가 NULL이라면
if(x == NULL)
{
root = init();
x = root;
}
// 루트 노드가 NULL이 아니라면
else
{
// 현재 리프노드이고 크기가 꽉찼다면
if(x->leaf == true && x->n == M)
{
temp = splitChild(x, -1);
x = root;
// 값을 이동하며 삽입될 자리를 찾습니다.
for(i = 0; i < (x->n); i++)
{
if((a > x->data[i]) && (a < x->data[i + 1]))
{
i++;
break;
}
else if(a < x->data[0])
{
break;
}
else
{
continue;
}
}
x = x->childPtr[i];
}
// 리프노드가 아닐 때입니다.
else
{
// 리프 노드까지 이동합니다.
while(x->leaf == false)
{
for(i = 0; i < (x->n); i++)
{
if((a > x->data[i]) && (a < x->data[i + 1]))
{
i++;
break;
}
else if(a < x->data[0])
{
break;
}
else
{
continue;
}
}
// 리프 노드 위에서도 만약에 최대치를 넘으면 분할해줍니다.
if((x->childPtr[i])->n == M)
{
temp = splitChild(x, i);
x->data[x->n] = temp;
x->n++;
continue;
}
else
{
x = x->childPtr[i];
}
}
}
}
x->data[x->n] = a;
sort(x->data, x->n);
x->n++;
}
int main(void)
{
int i, n, t;
cout << "삽입할 원소의 개수를 입력하세요 : ";
cin >> n;
for(i = 0; i < n; i++)
{
cout << "원소를 입력하세요 : ";
cin >> t;
insert(t);
}
cout << "트리를 순회합니다." << endl;
traverse(root);
return 0;
}
결과값

'알고리즘' 카테고리의 다른 글
| 해시 (체이닝, 개방주소) (0) | 2019.04.29 |
|---|---|
| kd-트리 (0) | 2019.04.29 |
| 레드블랙트리 (자가균형 이진탐색트리) (0) | 2019.04.15 |
| 이진 트리 탐색 (0) | 2019.04.07 |