2019. 5. 27. 16:34ㆍ알고리즘/그래프
최소 신장 트리
그래프 G=(V,E)의 신장 트리는 정점 집합 V를 그대로 두고 간선을 |V|-1개만 남겨 트리가 되도록 만든 것입니다.
임의의 그래프로부터 만들 수 있는 신장 트리는 매우 다양합니다. 너비 우선 트리와 깊이 우선 트리도 신장 트리입니다.
간선들이 가중치를 갖는 그래프에서 간선 가중치의 합이 가장 작은 트리를 최소 신장 트리라고 합니다.
밑은 최소신장 트리 종류중 하나인 프림 알고리즘입니다.
1. Prim's 알고리즘
Prim's 알고리즘은 최소 우선순위 큐에서 가중치가 가장 작은 정점을 선택한 후,
그 정점의 인접한 정점들에 대해 key 값과 연결된 가중치 값을 비교하여 key값을 갱신할 지 말지 결정합니다.

초기 그래프입니다.
모든 정점들의 key 값은 inf가 할당되어 있습니다.
그 이유는 Prim's 알고리즘이 최소 우선 순위 큐에서 각 정점의 key값들 중
최소 값을 뽑아 그 정점을 이용하여 다음 단계를 진행하게 되기 때문입니다.
그래서 어떠한 가중치보다 큰 값으로 설정하기 위해 inf를 할당합니다.

start vertex를 설정합니다.
Prim's 알고리즘은 어떤 vertex를 start로 하든 항상 같은 트리가 형성됩니다.
start vertex는 초기 값으로 key값을 0으로 할당합니다.

Step 2에서 큐에는 { 0, inf , inf , inf , inf , inf , inf } 원소들이 있고,
그 중에서 0이 가장 작으므로 start vertex가 선택됩니다.

선택된 vertex에 대해서 인접 간선의 가중치와 정점의 key 값을 확인합니다.
즉 Step 4 ~ Step 7은 하나의 큰 단계라고 보시면 됩니다.
수도 코드에서는 이를 반복문으로 표현하고 있습니다.
첫 번째로 가중치가 9인 간선을 확인합니다.
Step 3에서 start vertex와 가중치가 9인 간선으로 연결된 정점의 key 값은 inf였습니다.
즉 가중치 = 9 , key 값 = inf
9 < inf 이므로 정점의 key 값을 가중치의 값으로 바꿔줍니다.
이것이 Prim's 알고리즘이 MST를 만드는 규칙입니다.
그리고 key 값이 변경된 정점의 부모는 start vertex라는 것을 표현하기 위해 화살표로 표시하겠습니다.

다음으로 가중치가 6인 간선에 대해, Step 4의 과정을 수행합니다.
Step 4에서 가중치 값 = 6 < inf = key 값
이므로 key 값을 6으로 변경합니다.
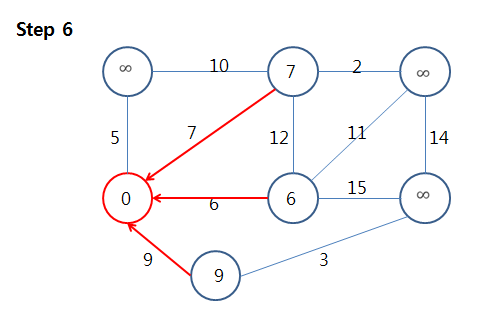
이전 단계와 같습니다.

이전 단계와 같습니다.

이제 start vertex에 대해서 모든 간선들을 확인해보았습니다.
그러면 이제 다음 정점을 선택하기 위해 최소 우선 순위 큐에서 key 값이 가장 작은 정점을 고릅니다.
지금 우선 순위 큐에는 { 5 , 7 , inf , 6 , inf , 9 } 가 있으므로 가장작은 값은 5입니다.
Step 9부터는 key 값이 5인 정점에 대해 Step 4 ~ Step 7의 과정을 수행할 것입니다.

key 값이 5인 정점과 연결된 간선들 보니 가중치가 10인 간선이 있고,
이 간선과 연결된 정점의 key 값은 7입니다.
가중치 = 10 > 7 = key 값
이므로 key 값을 변경하지 않습니다.
key 값을 변경하는 것은 가중치보다 key 값이 더 클 경우에만 해당됩니다.
연결된 간선이 1개 밖에 없으므로 다시 최소 우선순위 큐에서 또 정점을 골라야겠네요.

다음에 선택된 정점은 key 값이 6 정점입니다.
인접한 간선들의 가중치는 12 , 11 , 15 이네요.

Step 10에서 가중치가 15인 간선에 대해, 이 간선과 연결된 정점의 key 값은 inf이므로
가중치 = 15 < inf = key 값
따라서 key 값을 변경합니다.

이전 단계와 같습니다.

가중치 = 12 < 7 = key 값
이므로 key 값을 변경하지 않습니다.

우선순위 큐 중에서 값이 가장작은 정점이 선택됩니다.

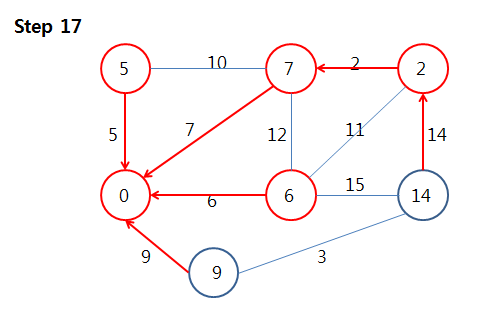
연결된 간선 중 가중치가 2인 간선에 대해, 연결된 정점의 key 값은 11입니다.
가중치 = 2 < 11 = key 값
이므로 key 값을 변경합니다.
이 때 key 값이 변경되는 정점은 이미 가중치가 11인 간선을 갖고 있었습니다.
그런데 key 값이 새로 변경되었으므로 부모를 갱신해야 합니다.
이제 더 특별한 것은 없으므로 이후의 과정은 생략하도록 하겠습니다.



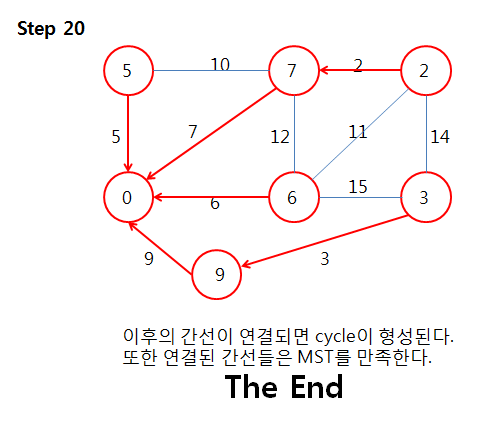
프림 알고리즘 수행 시간은 보통 O(V^2)입니다. 하지만 힙정렬을 사용하게 되면
O(ElogV)까지 줄일 수 있습니다.
<Graph>
package 그래프;
import java.util.HashMap;
import java.util.Map;
public class Graph {
private final String[] names = {"철수", "영희", "동건", "준호", "재상", "승우"};
private Map<String, Integer> vertex = new HashMap<>();
private int[][] edges;
Graph() {
for (int i = 0; i < names.length; i++) {
vertex.put(names[i], i);
}
edges = new int[][]{
{0, 9, 7, 5, 0, 6},
{9, 0, 9, 0, 0, 0},
{7, 9, 0, 0, 5, 0},
{5, 0, 0, 0, 0, 5},
{0, 0, 5, 0, 0, 1},
{6, 0, 0, 5, 1, 0}
};
}
Map<String, Integer> getVertex() {
return vertex;
}
int size() {
return names.length;
}
int getValue(String name) {
return vertex.get(name);
}
private int indexOf(String name) {
for(int i=0; i<names.length; i++) {
if (names[i].equals(name)) return i;
}
return -1;
}
public int[] getEdge(String name) {
int index = indexOf(name);
return edges[index];
}
int getCost(int i, int j) {
return edges[i][j];
}
String getName(int index) {
return names[index];
}
}
<MinimumSpanningTree>
package 그래프;
import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;
class MinimumSpanningTree {
private final static int INF = 9999;
static void prim(Graph g, String r) {
System.out.println("---- 최소 신장 트리 ----");
// 공집합 S 생성
Map<String, Integer> S = new HashMap<>();
// r을 집합 S에 삽입
S.put(r, g.getValue(r));
System.out.println(r);
// 집합 S와 전체 정점 집합이 동일해질 때까지 반복
while (!S.equals(g.getVertex())) {
// 집합 S에 연결된 정점들 중 비용이 가장 작은 정점 선택
int min = INF;
int from = 0;
int to = 0;
for (String key : S.keySet()) {
int i = S.get(key);
for(int j=0; j<g.size(); j++) {
if(S.containsKey(g.getName(j))) continue; // S 집합에 있으면 방문 했음을 의미하기에 통과
int cost = g.getCost(i, j);
if(min > cost && cost > 0) {
min = cost;
from = i;
to = j;
}
}
}
String v = g.getName(to);
S.put(v, g.getValue(v));
System.out.printf("%s(%d - %d)\n", v, from, to);
// 반복
}
}
}
<main>
package 그래프;
public class main {
public static void main(String[] args) {
MinimumSpanningTree.prim(new Graph(), "철수");
System.out.println();
}
}
결과

'알고리즘 > 그래프' 카테고리의 다른 글
| 위상정렬 알고리즘 (0) | 2019.05.27 |
|---|---|
| 그래프 탐색 (0) | 2019.05.20 |
| 그래프(Graph) (0) | 2019.05.20 |