2019. 3. 28. 20:08ㆍ알고리즘/정렬
힙정렬은 시간복잡도가 nlogn 으로 퀵정렬과 병합(합병)정렬과 같은 시간복잡도를 가진 정렬 알고리즘이다.
하지만 병합정렬과는 다르게 추가적인 메모리가 필요하지않고, 항상 nlogn의 정렬 성능을 보여주기때문에 최악의 경우 n^2 의 성능을 보이는 퀵정렬보다 안정적인 성능을 보인다.
힙정렬은 힙의 구조에 대해 알고있으면 생각보다 간단한 정렬이다.
힙정렬을 알아보기전에 힙(Heap) 에 대해 간단히 알아보자.
힙(Heap)
힙 트리 라고도 하는 힙은 완전이진트리 형태의 자료구조이다.
완전이진트리
노드를 삽일할때 왼쪽부터 차례대로 추가하는 이진트리(모든 노드의 차수가 2이하로 구성된 트리)
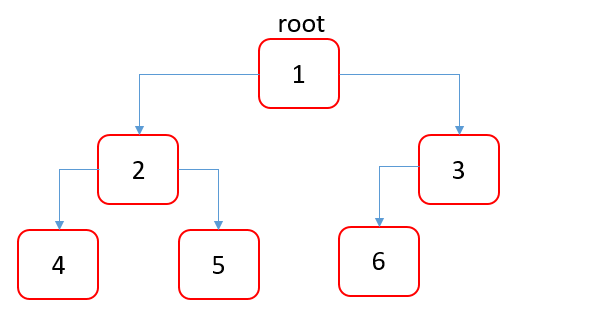
위와같은 트리가 완전이진트리이며(각노드의 왼쪽부터 채워진 이진트리) 아래는 그냥 이진트리.

힙에는 최소힙과 최대힙이 있으며 최소힙은 부모노드의 키값이 자식노드의 키값보다 작을때, 그반대가 최대힙이다.
그리고 힙은 일반적인 배열로 표현 할 수 있다.
a = {-1,3,4,5,1,7,2,8} //a[0]은 pass
이라는 배열이 있다.(a[1]부터 시작한다.) 루트노드는 항상 a[1] 번째일때 힙트리를 보면 다음과 같다.

각 노드의 자식노드는 다음과 같다는것을 알 수 있다. (단, root가 1번째 배열부터 시작할때이다. 0번째 배열부터면 +1추가해줘야 식이성립함)
※부모노드 = i / 2 (i>0) ( ex. A[3]의 부모노드 = A[i/2] = A[1.5](정수형) = A[1] )
※왼쪽자식노드 = i * 2 ( ex. A[3]의 왼쪽 자식노드 = A[i*2] = A[6] )
※오른쪽자식노드 = i * 2 + 1 ( ex. A[3]의 오른쪽 자식노드 = A[i*2+1] = A[7] )
이같은 규칙때문에 배열로봐도 힙구조가 나온다.
A[1] A[2] A[3] A[4] A[5] A[6] A[7] { -1 , 3 , 4 , 5 , 1 , 7 , 2 , 8 }
힙에대해 알아보았따..
그럼이제 힙을이용해 정렬을 하려면 이 힙을 최소힙이나 최대힙으로 만들어주어야한다.
힙정렬의 원리는 최소힙이나 최대힙이 되었을때 root 는 항상 힙에서 최대값 또는 최소값이 나오게되어있다. 이때 root 를 힙의 마지막 노드와 교체한 뒤 힙의 마지막을 제외한 힙으로 다시 최소힙이나 최대힙을 구성하고 나온 root(최소값 또는 최대값) 을 마지막 노드와 교체하는 방식으로 정렬을한다.
힙정렬 의 순서를 요약하여 살펴보면
1. 정렬되지않은 배열 생성
2. 최소힙 또는 최대힙 구성
3. root 를 마지막노드와 교체
4. 2~3 반복
#include <iostream>
using namespace std;
//힙정렬
int n, heap[10000001];
void heapify(int i)
{
int cur = 2 * i;
if (cur < n && heap[cur] < heap[cur + 1]) cur++;
if (heap[i] < heap[cur])
{
swap(heap[i], heap[cur]);
if (cur <= n / 2) heapify(cur);
}
}
void heapsort(int i)
{
swap(heap[1], heap[i]);
int root = 1;
int cur = 2;
while (cur / 2 < i)
{
cur = 2 * root;
if (cur < i - 1 && heap[cur] < heap[cur + 1]) cur++;
if (cur < i && heap[root] < heap[cur])
swap(heap[root], heap[cur]);
root = cur;
}
}
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
cin >> heap[i];
for (int i = n / 2; i > 0; i--) // 최초 heap 생성
heapify(i);
for (int i = n; i > 0; i--) // heap 정렬
heapsort(i);
for (int j = 1; j <= n; j++) // 출력
cout << heap[j] << " ";
system("pause");
}
결과 값
'알고리즘 > 정렬' 카테고리의 다른 글
| 정렬 알고리즘 시간복잡도 (0) | 2019.03.28 |
|---|---|
| 평균 선형 시간 선택 알고리즘 (0) | 2019.03.28 |
| 퀵 정렬(Quick Sort) (0) | 2019.03.28 |
| 병합정렬(merge sort) (0) | 2019.03.28 |
| 삽입 정렬(insertion sort) (0) | 2019.03.28 |